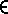 { =,
{ =,  }
}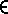 { <,
=, > }
{ <,
=, > }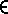 { =r*
| r
{ =r*
| r 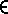 R }
R }
Yuri Engelhardt
Institute for Logic, Language, and Computation
University of Amsterdam, The Netherlands
yuri@wins.uva.nl
Introduction
Diagrams, maps, tables, charts and graphs use perceptual attributes such as shape, color, size and spatial position to create meaningful perceptual structures. It seems intuitively obvious that a good visualization exposes the 'structure' of the information that represents. In other words: We expect a good visualization to be a 'structure-preserving' mapping between an information domain and a perceptual domain. But what exactly do we mean by 'structure'? What exactly is preserved in a good visualization?
As Bertin (1981) has pointed out, information is about relationships between things, and - similarly - a graphic is about relationships between graphical marks. In search of structure preservation in graphics, we therefore examine relationships between elements, rather than the elements in isolation. Bertin claims that there are three graphically expressible relationships: resemblance, order and proportion. However, he does not define these relationships in any formal manner, let alone integrate his individual explanations of them in a systematic way.
In this short paper we confine ourselves to the visualization of functional two-place relations. For such data we present a general, simple way to accurately represent the above mentioned kinds of relationships (see below, formula 1). We state that it is the structure that is specified by such relationships, that is preserved in good visualizations. This leads us to a definition of structure-preserving visualization (see below, formula 2).
Representing relationships with compare operators
Examples of relationships between data elements are "comes from the same country as" or "is five times as expensive as". Examples of relationships between graphical elements are "has the same color as" or "has five times the size of". We refer to "same" and "five times" as compare-operators. A compare-operator compares to elements with regard to a given attributes.
A relational database involves data elements (e.g. Mary, John) and individual names (e.g. female, 30 years) for their data attributes (e.g. gender, age). Depending on the domain of these attributes, we can infer from such a database different kinds of relationships between elements. Such inferred relationships between elements can be represented in the format:
It is the structure described by such relationships, that is preserved in a good visualization. Different types of data attributes (as distinguished by Stevens 1946, Bertin 1981, Mackinlay 1986, Roth & Mattis 1990) allow different compare-operators (cop). Examples:
| Categorical Attributes | cop 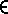 { =, { =,  }
} |
| Ordinal attributes | cop 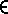 { <,
=, > } { <,
=, > } |
| Ratio Attributes | cop 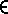 { =r*
| r { =r*
| r 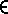 R } R } |
These sets of compare-operators play the key role in structure-preserving visualization.
From data structure to perceptual structure
Definition:
A graphic is a structure-preserving visualization of given data if for all x,y and att it holds that:
| att(x) cop att(y) | 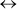 |
att'(x') cop att'(y') | (2) |
In this definition, all compare-operators (cop) from the data structure have to be preserved in the perceptual structure. Here are some possible examples, expressed in the above formula (2):
| gender(x) |  |
gender(y) | 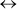 |
color-hue(x') |  |
color-hue(y') |
| skill-level(x) | > | skill-level(y) | 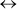 |
saturation(x') | > | saturation(y') |
| age(x) | =2* | age(y) | 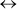 |
size(x') | =2* | size(y') |
According to the above definition, a structure-preserving mapping from a data attribute (att) to a perceptual attribute (att') will only be possible if both of the same compare-operators (cop). Below is example list of the compare-operators that are available to the human observer for various perceptual attributes (see Bertin 1981, Mckinlay 1986):
| shape, color hue: | cop 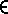 { =, { =,  }
} |
(categorical) | (Bertin: resemblance) |
| color saturation: | cop 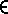 { <,
=, > } { <,
=, > } |
(ordinal) | (Bertin: order) |
| size, slider position: | cop 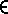 { =r*
| r { =r*
| r 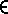 R } R } |
(ratio) | (Bertin: proportion) |
If a perceptual attribute supports the same compare-operators (cop) as a given data attribute, then the structure-preserving mapping between these two attributes is possible. Complex visualizations are the result of combining several structure-preserving, attribute-to-attribute mappings.
Conclusion
In the introduction we asked: What exactly is preserved in a good visualization? We can now offer an answer: For each visualized attribute, a good visualization preserves the structure of the relationships between the elements. More specifically, this is achieved by preserving - for each of the visualizeed attributes - the concerned compare-operators between elements.
References
[1] Bertin, J. (1981) Graphics and graphic information processing. Walter de Gruter, Berlin. Pages 176, 177 and 180.
[2] Mackinlay, J. (1986): Automating the design of graphical presentations of relational information. ACM Transactions on Graphics, Vol. 5, No. 2. Pages 110-141.
[3] Roth, S.F. and Mattis, J. (1990): Data characterization for intelligent graphics presentation. Proceedings SIGCHI '90, Seattle (WA), ACM Press. Pages 193-200.
[4] Stevens, S.S. (1946): On the theory of scales of measurement. Science, 103. Pages 677-680.